
Given:-
- Radius of the circle = 10 inches
- Angle of each sector = 72°
- Number of sectors = 2
To FinD:-
- Find the area of the shaded regions....?
How to solve?
For solving this question, Let's know how to find the area of a sector in a circle?
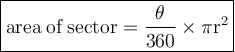
Here, Θ is the angle of sector and r is the radius of the circle. So, let's solve this question.
Solution:-
We have,
- No. of sectors = 2
- Angle of sector = 72°
By using formula,
⇛ Area of shaded region = 2 × Area of each sector
⇛ Area of shaded region = 2 × Θ/360° × πr²
⇛ Area of shaded region = 2 × 72°/360° × 22/7 × 10²
⇛ Area of shaded region = 2/5 × 100 × 22/7
⇛ Area of shaded region = 40 × 22/7
⇛ Area of shaded region = 880/7 inch. sq.
⇛ Area of shaded region = 125.71 inch. sq.
☄ Your Required answer is 125.71 inch. sq(approx.)
━━━━━━━━━━━━━━━━━━━━