Question

Find the area of the shaded regions:

Answer 1

area of Arc subtending
`360^(\circ)` (i.e. the whole circle) is $\pi r^2$

so area of Arc subtending $\theta^{\circ}$ is, $\frac{ \pi r^2}{360^{\circ}}\times \theta^{\circ}$

$\theta =72^{\circ}$ so the area enclosed by one such arc is $\frac{\pi (10)^272}{360}$

abd there are 2 such arcs, so double the area.

Answer 2

`\LARGE{ \underline{ \boxed{ \rm{ \purple{Solution}}}}}`

Given:-

• Radius of the circle = 10 inches
• Angle of each sector = 72°
• Number of sectors = 2

To FinD:-

• Find the area of the shaded regions....?

How to solve?

For solving this question, Let's know how to find the area of a sector in a circle?

`\large{ \boxed{ \rm{area \: of \: sector = (\theta)/(360) * \pi {r}^(2) }}}`

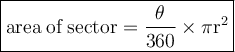
Here, Θ is the angle of sector and r is the radius of the circle. So, let's solve this question.

Solution:-

We have,

• No. of sectors = 2
• Angle of sector = 72°

By using formula,

⇛ Area of shaded region = 2 × Area of each sector

⇛ Area of shaded region = 2 × Θ/360° × πr²

⇛ Area of shaded region = 2 × 72°/360° × 22/7 × 10²

⇛ Area of shaded region = 2/5 × 100 × 22/7

⇛ Area of shaded region = 40 × 22/7

⇛ Area of shaded region = 880/7 inch. sq.

⇛ Area of shaded region = 125.71 inch. sq.

☄ Your Required answer is 125.71 inch. sq(approx.)

━━━━━━━━━━━━━━━━━━━━