Answer:
Explanation:
Hello, we know that if the equation is

Then the vertex is the the point (h,k)
Here, the vertex is the point (-2,-20) so we can write, a being a real number that we will have to find,
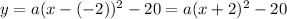
On the other hand, we know that the y-intercept is (0,-12) so we can write
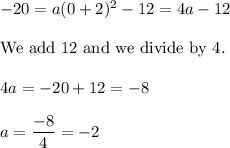
So the equation becomes.

And we can give the standard form as below.
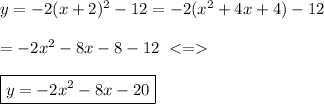
Thank you.