Question

Give this problem a try and try to solve this​

Answer 1

Could you please help me Genius??????

Answer 2

No solution

Explanation:

Given equation is,

`\frac{x^{(1)/(2)}+x^{-(1)/(2)}}{1-x}+\frac{1-x^{-(1)/(2)}}{1+x^(1)/(2)}-((4+x)^(1)/(2))/((1-x)^(1)/(2))=0`

`\frac{x^{(1)/(2)}+x^{-(1)/(2)}}{1-x}+\frac{1-x^{-(1)/(2)}}{1+x^(1)/(2)}=((4+x)^(1)/(2))/((1-x)^(1)/(2))`

`((x+1))/(√(x)(1-x))+((√(x)-1))/(√(x)(1+√(x)))=((4+x)/(1-x))^{(1)/(2)}`

`((√(x)+1)(x+1)+(√(x)-1)(1-x))/(√(x)(1-x)(1+√(x)))=((4+x)/(1-x))^{(1)/(2)}`

`(x√(x)+x+√(x)+1+√(x)-1-x√(x)+x)/(√(x)(1-x)(1+√(x)))=((4+x)/(1-x))^(1)/(2)`

`(2x+2√(x))/(√(x)(1-x)(1+√(x)))=((4+x)/(1-x))^(1)/(2)`

`(2(√(x)+1))/((1-x)(1+√(x)))=((4+x)/(1-x))^(1)/(2)`

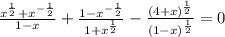
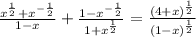
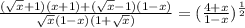
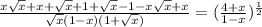
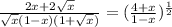
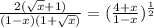
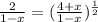`(2)/(1-x)=((4+x)/(1-x))^(1)/(2)` if x ≠ ±1

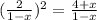`((2)/(1-x))^2=(4+x)/(1-x)` [Squaring on both the sides of the equation]

`(4)/((1-x))=(4+x)`

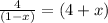
4 = (1 - x)(4 + x)

4 = 4 - 4x + x - x²

0 = -3x - x²

x² + 3x = 0

x(x + 3) = 0

x = 0, -3

But both the solutions x = 0 and x = -3 are extraneous solutions, given equation has no solution.