Question

1. Cases Prudence has a special (cubic) die. The values on its face are the integers from 1 to 6, but they are not arranged ae in a normal die. When Prudence first tosses the die, the sum of the values on the four side faces is 15. In her second toss, the sum of these values is 12. Find what value appears in the face opposite 6 on Prudence’s special die. (Hint: what are possible values for the top and bottom face when the sum of the side faces is 12).

Answer 1

The definition of the subject in question is presented in section elsewhere here.

Step-by-step explanation:

The total value of almost all of the quantities mostly on unique die features will indeed be:

⇒
`1+2+3+4+5+6`

⇒
`21`

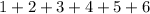
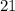
The number of the 4 lateral sides throughout the first tossing will be 15, therefore determines the total of both top and bottom features would be:

⇒
`21-15`

⇒
`6`

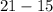
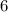
The compositions including its {top and bottom} current valuations that give a total of Six include {1, 5}, {5, 1}, {2, 4}, as well as {4, 2}. Consequently, because neither of those variations includes Six, it indicates that six doesn't really feature on the very first toss mostly on high or low hand.

And then let's look at second tossed situation. Throughout this particular instance, the total amount obtained would be 12.

Which means it has to be the number of top and bottom:

⇒
`21-12`

⇒
`9`

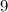
{4, 5},{5, 4}, {6, 3}, and {3, 6} seem to be the {top, bottom} facial variations that provide a total of Nine.

Currently regarding all the tosses, {6, 3} and perhaps {3, 6} have been the only situations wherein the 6 emerge towards top or bottom. Then the value of the unique die mostly on face identical to 6 must've been 3.