Answer:
The time it takes the rock to reach the canyon floor is approximately 4 seconds.
Explanation:
The equation representing the height h (in feet) of an object t seconds after it is dropped is:
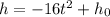
Here, h₀ is the initial height of the object.
It is provided that a small rock dislodges from a ledge that is 255 ft above a canyon floor.
That is, h₀ = 255 ft.
So, when the rock to reaches the canyon floor the final height will be, h = 0.
Compute the time it takes the rock to reach the canyon floor as follows:
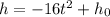
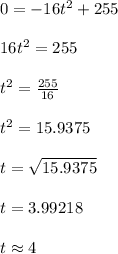
Thus, the time it takes the rock to reach the canyon floor is approximately 4 seconds.