Question

A Gallup poll asked 1200 randomly chosen adults what they think the ideal number of children for a family is. Of this sample, 53% stated that they thought 2 children is the ideal number.

Answer 1

A Gallup poll asked 1200 randomly chosen adults what they think the ideal number of children for a family is. Of this sample, 53% stated that they thought 2 children is the ideal number. Construct and interpret a 95% confidence interval for the proportion of all US adults that think 2 children is the ideal number.

Answer:

at 95% Confidence interval level: 0.501776 < p < 0.558224

Explanation:

sample size n = 1200

population proportion
`\hat p`= 53% - 0.53

At 95% confidence interval level;

level of significance ∝ = 1 - 0.95

level of significance ∝ = 0.05

The critical value for
`z_(\alpha/2) = z _(0.05/2)`

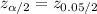
the critical value
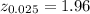`z _(0.025)= 1.96` from the standard normal z tables

The standard error S.E for the population proportion can be computed as follows:

`S,E = \sqrt{(\hat p * (1-\hat p))/(n)}`

`S,E = \sqrt{(0.53 * (1-0.53))/(1200)}`

`S,E = \sqrt{(0.53 * (0.47))/(1200)}`

`S,E = \sqrt{(0.2491)/(1200)}`

`S,E = 0.0144`

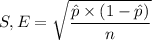
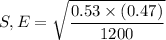
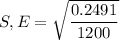
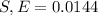
Margin of Error E=
`z_(\alpha/2) * S.E`

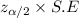
Margin of Error E= 1.96 × 0.0144

Margin of Error E= 0.028224

Given that the confidence interval for the proportion is 95%

The lower and the upper limit for this study is as follows:

Lower limit:
`\hat p - E`

Lower limit: 0.53 - 0.028224

Lower limit: 0.501776

Upper limit:
`\hat p + E`

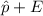
Upper limit: 0.53 + 0.028224

Upper limit: 0.558224

Therefore at 95% Confidence interval level: 0.501776 < p < 0.558224