Question

Please help ASAP. The question is down below.

Answer 1

Question 1.

Option A: 2m

Question 2

Option D: (1, 1) minimum point

Explanation:

Question 1.

Let the original length of the garden (before expansion) be = x

The new length of the garden will be x + 10m

Recall that the garden has a square geometry. That means that its area is obtained by squaring any of its sides.

This means that
`(x +10)^2 = 144`

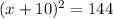
We can now solve for x

`(x +10)^2 = 144\\x^2 +20x +100 = 144\\x^2 + 20x =44\\x^2 + 20x - 44=0\\x = 2 or -22`

x cannot be a negative number, so the original length of a side of the garden is 2m. Option A

Question 2:

The coordinates of the vertex of the graph (turning point) are (x, y) [1,1]

To know whether it is a minimum or maximum point, we will have to check the coefficient of
`x^2` in the equation
`y = x^2-2x+2`

The coefficient of
`x^2` in the equation is 1. (If no number is present, just know that the coefficient is a one).

If the coefficient is positive, then the point is a minimum point. However, if it is negative, then the point is a maximum point.

Our coefficient is positive hence, the graph has a minimum point.