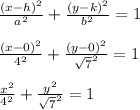Answer:
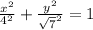
Explanation:
Since the vertex of the parabola is at (4,0), it has the vertex on the x axis (horizontal axis). The standard equation of an ellipse with horizontal major axis is given by:
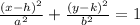
Where (h,k) is the center of the ellipse, a is the vertex and ±√(a²- b²) is the focus (c).
Since the ellipse center is at (0, 0), h = 0 and k = 0. Also the vertex is at (4, 0) therefore a = 0
To find b we use the equation of the focus which is:
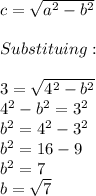
Substituting the values of a, b, h and k: