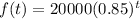Answer:
Explanation:
So the initial value of the business computer is $20,000. It depreciates by 15% per year. This is exponential decay. The standard function for exponential decay is:
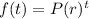
Where P is the initial value, r is the rate of decay, and t is the time in years.
Since the computer decreases by 15% per year, this means that each year, the computer will be 1-15% or 85% than its previous value.
Therefore, the equation that models the value of the computer is: