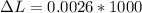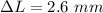Answer:
a
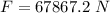
b
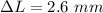
Step-by-step explanation:
From the question we are told that
The Young modulus is
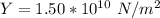
The stress is
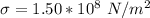
The diameter is
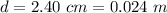
The radius is mathematically represented as
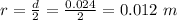
The cross-sectional area is mathematically evaluated as
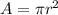
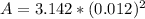
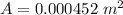
Generally the stress is mathematically represented as
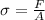
=>
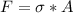
=>
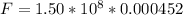
=>
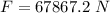
Considering part b
The length is given as
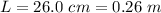
Generally Young modulus is mathematically represented as
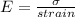
Here strain is mathematically represented as
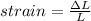
So
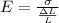
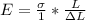
=>
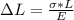
substituting values
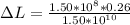
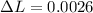
Converting to mm