Question

`\frac{ {9x}^(2) - {(x}^(2) - 4) {}^(2) }{4 + 3x - {x}^(2) }`

pls help me need help asap

Answer 1

`{ x^2+3x-4}`

Explanation:

Factor top and bottom.

The numerator is a difference of two squares, and the denominator is a quadratic.

`\frac{ {9x}^(2) - {(x}^(2) - 4)^(2) }{4 + 3x - {x}^(2) }`

=
`( (3x+x^2-4)(3x-x^2+4) )/((1+x)(4-x))`

=
`( (x-1)(x+4) (1+x)(4-x) )/((1+x)(4-x))`

If x does not equal -1 and does not equal 4, we can cancel the common factors in italics to give

=
`{ (x-1)(x+4)}`

=
`{ x^2+3x-4}`

Answer 2

The answer is

x² + 3x - 4

Explanation:

`\frac{9 {x}^(2) - ( { {x}^(2) - 4})^(2) }{4 + 3x - {x}^(2) }`

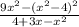
To solve the expression first factorize both the numerator and the denominator

For the numerator

9x² - ( x² - 4)²

Expand the terms in the bracket using the formula

( a - b)² = a² - 2ab + b²

(x² - 4) = x⁴ - 8x² + 16

So we have

9x² - (x⁴ - 8x² + 16)

9x² - x⁴ + 8x² - 16

- x⁴ + 17x² - 16

Factorize

that's

(x² - 16)(-x² + 1)

Using the formula

a² - b² = ( a + b)(a - b)

We have

(x² - 16)(-x² + 1) = (x + 4)(x - 4)( 1 - x)(1 + x)

For the denominator

- x² + 3x + 4

Write 3x as a difference

- x² + 4x - x + 4

Factorize

That's

- ( x - 4)(x + 1)

So we now have

`((x + 4)(x - 4)( 1 - x)(1 + x))/( - (x - 4)(x + 1))`

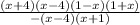
Simplify

`( - (x + 4)(1 - x)(1 + x))/(x + 1)`

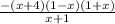
Reduce the expression by x + 1

That's

-( x + 4)( 1 - x)

Multiply the terms

We have the final answer as

x² + 3x - 4

Hope this helps you