Question

(1-Cota)^2

+(tana-1)^2=4cosec2a(cosec2a-1)
​

Answer 1

Explanation:

(1-CotA)² + (tanA-1)² = 4csc2A(csc2A-1)

To prove this equation we will take the expression given in left hand side and will convert it into the expression given in right hand side of the equation.

L.H.S. = (1-CotA)² + (tanA-1)²

= 1 + Cot²A - 2CotA + 1 + tan²A - 2tanA

= cosec²A - 2CotA + Sec²A - 2tanA

[Since, (1 + Cot²A = cosec²A) and (1 + tan²A = Sec²A)]

= (cosec²A + Sec²A) - 2(CotA + tanA)

=
`(\frac{1}{\text{SinA}})^(2)+((1)/(CosA) )^(2)-2\text{(tanA}+\frac{1}{\text{tanA}})}`

=
`\frac{1}{(\text{SinA.CosA})^2}-2((tan^2A+1)/(tanA) )`

=
`\frac{4}{\text{(Sin2A})^(2)}-4(\frac{1}{\text{Sin2A}} )`

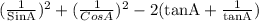
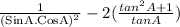
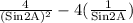
[Since 2SinA.CosA = Sin2A and
`\frac{2(\text{tanA})}{1+\text{tan}^(2)A}=\text{Sin2A}`]

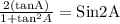= 4Cosec²2A - 4Cosec2A

= 4Cosec2A(Cosec2A - 1)

= R.H.S. (Right hand side)

Hence the equation is proved.