Answer:
Explanation:
(1-CotA)² + (tanA-1)² = 4csc2A(csc2A-1)
To prove this equation we will take the expression given in left hand side and will convert it into the expression given in right hand side of the equation.
L.H.S. = (1-CotA)² + (tanA-1)²
= 1 + Cot²A - 2CotA + 1 + tan²A - 2tanA
= cosec²A - 2CotA + Sec²A - 2tanA
[Since, (1 + Cot²A = cosec²A) and (1 + tan²A = Sec²A)]
= (cosec²A + Sec²A) - 2(CotA + tanA)
=
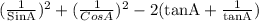
=
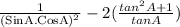
=
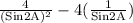
[Since 2SinA.CosA = Sin2A and
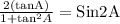 ]
]
= 4Cosec²2A - 4Cosec2A
= 4Cosec2A(Cosec2A - 1)
= R.H.S. (Right hand side)
Hence the equation is proved.