Answer:
Explanation:
I'm assuming you are trying to solve for x. I'm not sure, but that's what I figured out for the answer, so I'm gonna go with that. : )
We are looking for the value of x to make that statement true. It's going to take some trig manipulations, but if you are at this level of precalc, these identities should definitely NOT be new to you. We will begin by squaring both sides of that equation to get:
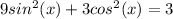
From here we will factor out a 3 to get:
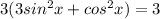 and then divide both sides by 3 to get:
and then divide both sides by 3 to get:

Knowing the Pythagorean identity for the trig ratios, we will replace the sin-squared with what it is equal to in terms of cos-squared. If:
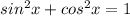 , then
, then
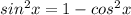 . Making that replacement gives us an equation with only one trig ratio in it, namely, cos:
. Making that replacement gives us an equation with only one trig ratio in it, namely, cos:
 and distributing:
and distributing:
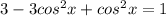 which simplifies down to:
which simplifies down to:
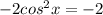 . Divide both sides by -2 to get:
. Divide both sides by -2 to get:
 . When you take the square root of both sides you get:
. When you take the square root of both sides you get:
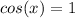 and
and
 . Here is where we will use the unit circle to see where the cos is 1 and where the cos is -1. You didn't give me an interval in which to work, so I am going to use from 0 degrees to 180. Within that interval, the cos is 1 at 0 degrees; within that interval, the cos is -1 at 180.
. Here is where we will use the unit circle to see where the cos is 1 and where the cos is -1. You didn't give me an interval in which to work, so I am going to use from 0 degrees to 180. Within that interval, the cos is 1 at 0 degrees; within that interval, the cos is -1 at 180.
Now we need to plug those values into the original equation to see if they work. One of them may be extraneous. Plugging in 0 first:
3sin(0) + √3cos(0) = -√3. We need to see if this is true.
The sin of 0 is 0; the cos of 0 is 1, so
0 + (√3)(1) = -√3?
The left side is √3, not -√3, so 0 doesn't work. Let's try 180 now, shall we?
3sin(180) + √3cos(180) = -√3. We need to see if this is true.
The sin of 180 is 0; the cos of 180 is -1, so
0 + (√3)(-1) = -√3?
The left side is -√3 and so is the right side, so
x = 180°