Answer:
See below.
Explanation:
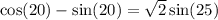
First, use the co-function identity:
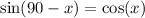
We can turn the second term into cosine:
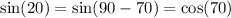
Substitute:
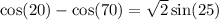
Now, use the sum to product formulas. We will use the following:
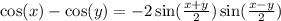
Substitute:
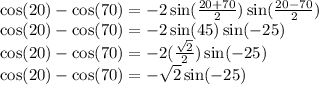
Use the even-odd identity:
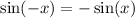
Therefore:
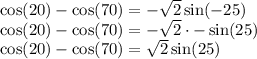
Replace the second term with the original term:
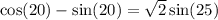
Proof complete.