Question

PROVE THAT:

cos 20° - sin 20° = ​​ \sqrt{2}sin25°

​

Answer 1

See below.

Explanation:

`\cos(20)-\sin(20)=√(2)\sin(25)`

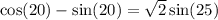
First, use the co-function identity:

`\sin(90-x)=\cos(x)`

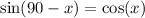
We can turn the second term into cosine:

`\sin(20)=\sin(90-70)=\cos(70)`

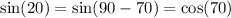
Substitute:

`\cos(20)-\cos(70)=√(2)\sin(25)`

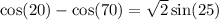
Now, use the sum to product formulas. We will use the following:

`\cos(x)-\cos(y)=-2\sin((x+y)/(2))\sin((x-y)/(2))`

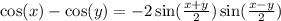
Substitute:

`\cos(20)-\cos(70)=-2\sin((20+70)/(2))\sin((20-70)/(2))\\\cos(20)-\cos(70) =-2\sin(45)\sin(-25)\\\cos(20)-\cos(70)=-2((√(2))/(2))\sin(-25)\\ \cos(20)-\cos(70)=-√(2)\sin(-25)`

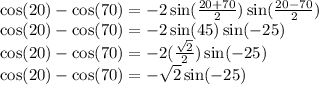
Use the even-odd identity:

`\sin(-x)=-\sin(x)`

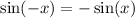
Therefore:

`\cos(20)-\cos(70)=-√(2)\sin(-25)\\\cos(20)-\cos(70)=-√(2)\cdot-\sin(25)\\\cos(20)-\cos(70)=√(2)\sin(25)`

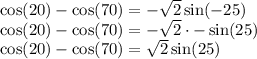
Replace the second term with the original term:

`\cos(20)-\sin(20)=√(2)\sin(25)`

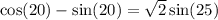
Proof complete.