Answer: Tension = 47.8N, Δx = 11.5×
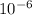 m.
m.
Tension = 95.6N, Δx = 15.4×
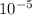 m
m
Step-by-step explanation: A speed of wave on a string under a tension force can be calculated as:
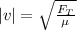
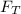 is tension force (N)
is tension force (N)
μ is linear density (kg/m)
Determining velocity:
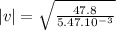
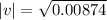
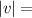 0.0935 m/s
0.0935 m/s
The displacement a pulse traveled in 1.23ms:
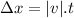
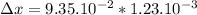
Δx = 11.5×
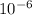
With tension of 47.8N, a pulse will travel Δx = 11.5×
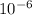 m.
m.
Doubling Tension:
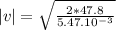
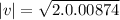
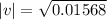
|v| = 0.1252 m/s
Displacement for same time:
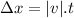
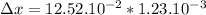
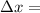 15.4×
15.4×
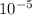
With doubled tension, it travels
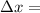 15.4×
15.4×
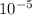 m
m