Question

10. How far does a transverse pulse travel in 1.23 ms on a string with a density of 5.47 × 10−3 kg/m under tension of 47.8 ????? How far will this pulse travel in the same time if the tension is doubled?

Answer 1

Answer: Tension = 47.8N, Δx = 11.5×
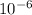`10^(-6)` m.

Tension = 95.6N, Δx = 15.4×
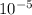`10^(-5)` m

Step-by-step explanation: A speed of wave on a string under a tension force can be calculated as:

`|v| = \sqrt{(F_(T))/(\mu) }`

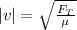
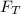`F_(T)` is tension force (N)

μ is linear density (kg/m)

Determining velocity:

`|v| = \sqrt{(47.8)/(5.47.10^(-3)) }`

`|v| = √(0.00874 )`

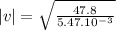
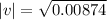
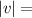`|v| =` 0.0935 m/s

The displacement a pulse traveled in 1.23ms:

`\Delta x = |v|.t`

`\Delta x = 9.35.10^(-2)*1.23.10^(-3)`

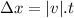
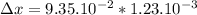
Δx = 11.5×
`10^(-6)`

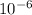
With tension of 47.8N, a pulse will travel Δx = 11.5×
`10^(-6)` m.

Doubling Tension:

`|v| = \sqrt{(2*47.8)/(5.47.10^(-3)) }`

`|v| = √(2.0.00874 )`

`|v| = √(0.01568)`

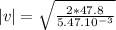
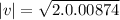
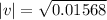
|v| = 0.1252 m/s

Displacement for same time:

`\Delta x = |v|.t`

`\Delta x = 12.52.10^(-2)*1.23.10^(-3)`

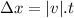
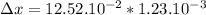
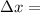`\Delta x =` 15.4×
`10^(-5)`

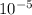
With doubled tension, it travels
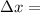`\Delta x =` 15.4×
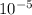`10^(-5)` m