Question

Please help!!!

Simplify: (sin 0 - cos 0)2 + (sin 0 + cos 0)2 (5 points)
Select one:
a. 1
b. 2
c. sin^2theta
d. cos^2theta

Answer 1

B

Explanation:

(To save time, I'm going to use x instead of θ)

So we have the expression:

`(\sin(x)-\cos(x))^2+(\sin(x)+\cos(x))^2`

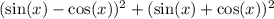
First, expand these binomials:

`=(\sin^2(x)-2\sin(x)\cos(x)+\cos^2(x))+(\sin^2(x)+2\sin(x)\cos(x)+\cos^2(x))`

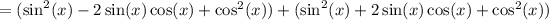
Combine like terms:

`=\sin^2(x)+\sin^2(x)+\cos^2(x)+\cos^2(x)-2\sin(x)\cos(x)+2\sin(x)\cos(x)\\=2\sin^2(x)+2\cos^2(x)`

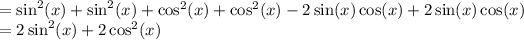
Factor out a 2:

`=2(\sin^2(x)+\cos^2(x))`

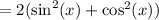
The expression inside the parentheses is the Pythagorean Identity:

`\sin^2(x)+\cos^2(x)=1`

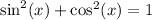
Substitute:

`=2(1)\\=2`

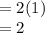
The answer is B.