Answer:
The final temperature is 61.65 °C
Step-by-step explanation:
mass of copper pot
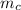 = 2 kg
= 2 kg
temperature of copper pot
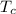 = 20 °C (the pot will be in thermal equilibrium with the room)
= 20 °C (the pot will be in thermal equilibrium with the room)
specific heat capacity of copper
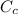 = 385 J/kg-°C
= 385 J/kg-°C
The heat content of the copper pot =
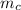
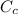
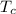 = 2 x 385 x 20 = 15400 J
= 2 x 385 x 20 = 15400 J
mass of boiling water
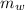 = 200 g = 0.2 kg
= 200 g = 0.2 kg
temperature of boiling water
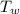 = 100 °C
= 100 °C
specific heat capacity of water
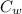 = 4182 J/kg-°C
= 4182 J/kg-°C
The heat content of the water =
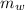
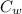
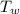 = 0.2 x 4182 x 100 = 83640 J
= 0.2 x 4182 x 100 = 83640 J
The total heat content of the water and copper mix
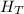 = 15400 + 83640 = 99040 J
= 15400 + 83640 = 99040 J
This same heat is evenly distributed between the water and copper mass to achieve thermal equilibrium, therefore we use the equation
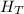 =
=
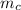
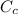
 +
+
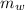
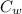
where
 is the final temperature of the water and the copper
is the final temperature of the water and the copper
substituting values, we have
99040 = (2 x 385 x
 ) + (0.2 x 4182 x
) + (0.2 x 4182 x
99040 = 770
 + 836.4
+ 836.4
99040 = 1606.4

 = 99040/1606.4 = 61.65 °C
= 99040/1606.4 = 61.65 °C