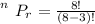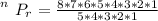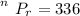Question

In the Cash Now lottery game there are 8 finalists who submitted entry tickets on time. From these 8 tickets, three grand prize winners will be drawn. The first prize is one million dollars, the second prize is one hundred thousand dollars, and the third prize is ten thousand dollars. Determine the total number of different ways in which the winners can be drawn. (Assume that the tickets are not replaced after they are drawn.)

Answer 1

The number of ways is
`\left n} \atop {}} \right. P_r = 336`

Explanation:

From the question we are told that

The number of tickets are
`n = 8`

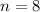
The number of finalist are
`r =3`

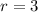
Generally the number of way by which this winners can be drawn and arrange in the order of
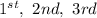`1^(st) , \ 2nd , \ 3rd` is mathematically represented as

`\left n} \atop {}} \right. P_r = (n\ !)/((n-r) !)`

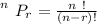
substituting values

`\left n} \atop {}} \right. P_r = ( 8!)/((8-3) !)`

`\left n} \atop {}} \right. P_r = ( 8* 7*6*5*4*3*2*1)/( 5*4*3*2*1)`

`\left n} \atop {}} \right. P_r = 336`