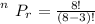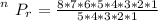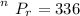Answer:
The number of ways is
Explanation:
From the question we are told that
The number of tickets are
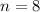
The number of finalist are
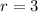
Generally the number of way by which this winners can be drawn and arrange in the order of
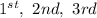 is mathematically represented as
is mathematically represented as
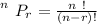
substituting values