Question

. Use the quadratic formula to solve each quadratic real equation. Round

your answers to two decimal places. If there is no real solution, say so.
a) x^2 - 5x + 11 = 0
b) -2x^2 - 7x + 15 = 0
c) 4x^2 - 44x + 121 = 0​

Answer 1

A. No real solution

B. 5 and -1.5

C. 5.5

Explanation:

The quadratic formula is:

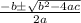`\begin{array}{*{20}c} {\frac{{ - b \pm \sqrt {b^2 - 4ac} }}{{2a}}} \end{array}`, with a being the x² term, b being the x term, and c being the constant.

Let's solve for a.

`\begin{array}{*{20}c} {\frac{{ 5 \pm \sqrt {5^2 - 4\cdot1\cdot11} }}{{2\cdot1}}} \end{array}`

`\begin{array}{*{20}c} {\frac{{ 5 \pm \sqrt {25 - 44} }}{{2}}} \end{array}`

`\begin{array}{*{20}c} {\frac{{ 5 \pm \sqrt {-19} }}{{2}}} \end{array}`

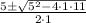
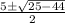
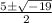
We can't take the square root of a negative number, so A has no real solution.

Let's do B now.

`\begin{array}{*{20}c} {\frac{{ 7 \pm \sqrt {7^2 - 4\cdot-2\cdot15} }}{{2\cdot-2}}} \end{array}`

`\begin{array}{*{20}c} {\frac{{ 7 \pm \sqrt {49 + 120} }}{{-4}}} \end{array}`

`\begin{array}{*{20}c} {\frac{{ 7 \pm \sqrt {169} }}{{-4}}} \end{array}`

`\begin{array}{*{20}c} {\frac{{ 7 \pm 13 }}{{-4}}} \end{array}`

`(7+13)/(4) = 5\\(7-13)/(4)=-1.5`

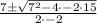
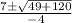
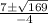
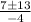
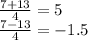
So B has two solutions of 5 and -1.5.

Now to C!

`\begin{array}{*{20}c} {\frac{{ -(-44) \pm \sqrt {-44^2 - 4\cdot4\cdot121} }}{{2\cdot4}}} \end{array}`

`\begin{array}{*{20}c} {\frac{{ 44 \pm \sqrt {1936 - 1936} }}{{8}}} \end{array}`

`\begin{array}{*{20}c} {\frac{{ 44 \pm 0}}{{8}}} \end{array}`

`(44)/(8) = 5.5`

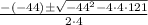
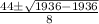
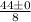
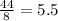
So c has one solution: 5.5

Hope this helped (and I'm sorry I'm late!)