Question

If you randomly select a card from a well-shuffled standard deck of 52 cards, what is the probability that the card you select is a heart or Ace

Answer 1

`P(A\ or\ H) = (4)/(13)`

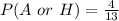
Explanation:

Given

Number of Cards = 52

Required

Determine the probability of picking a heart or ace

Represent Ace with Ace and Heart = H

In a standard pack of cards; there are

`n(A) = 4`

`n(H) = 13`

`n(A\ and\ H) = 1`

`Total = 52`

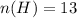
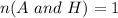
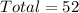
Because the events are non mutually exclusive

`P(A\ or\ H) = P(A) + P(H) - P(A\ and\ H)`

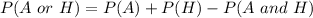
Where

`P(A) = (n(A))/(Total) = (4)/(52)`

`P(H) = (n(H))/(Total) = (13)/(52)`

`P(A\ and\ H) = (n(A\ and\ H))/(Total) = (1)/(52)`

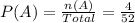
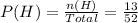
Substitute these values in the above formula

`P(A\ or\ H) = P(A) + P(H) - P(A\ and\ H)`

`P(A\ or\ H) = (4)/(52) + (13)/(52) - (1)/(52)`

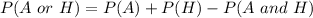
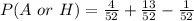
Take LCM

`P(A\ or\ H) = (4 + 13 - 1)/(52)`

`P(A\ or\ H) = (16)/(52)`

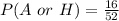
Reduce fraction to lowest term

`P(A\ or\ H) = (4)/(13)`

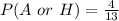
Hence, probability of a heart or ace is 4/13