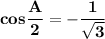Answer:
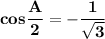
Explanation:
Given that:
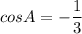
and

To find:

Solution:
First of all,we have cos value as negative and tan value as positive.
It is possible in the 3rd quadrant only.
 will lie in the 2nd quadrant so
will lie in the 2nd quadrant so
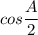 will be negative again.
will be negative again.
Because Cosine is positive in 1st and 4th quadrant.
Formula:
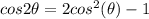
Here
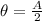
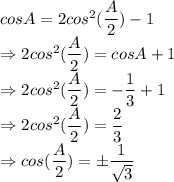
But as we have discussed,
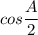 will be negative.
will be negative.
So, answer is: