Question

Use technology to solve the following problem: A certain car model has a mean gas mileage of 30 miles per gallon (mpg) with a standard deviation A pizza delivery company buys 42 of these cars. What is the probability that the average mileage of the fleet is greater than

Answer 1

The answer is below

Explanation:

The question is not complete, let me solve a question that is exactly like this one.

A certain car model has a mean gas mileage of 34 miles per gallon (mpg) with a standard deviation 5 mpg. A pizza delivery company buys 43 of these cars. What is the probability that the average mileage of the fleet is greater than 33.5 mpg?

Answer:

Given that the mean (μ) is 34 miles per gallon (mpg) with a standard deviation (σ) 5 mpg. The sample (n) is 43.

The z score is used in statistics to determine by how much the raw score is above or below the mean. It is given by:

`z=(x-\mu)/(\sigma) \\for\ a \ sample\ size:\\z=(x-\mu)/(\sigma/√(n) )`

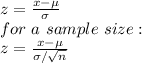
For the average mileage of the fleet is greater than 33.5 mpg (x > 33.5):

`z=(x-\mu)/(\sigma/√(n) )\\z=(33.5-34)/(5/√(43) ) =-0.66`

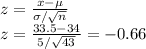
From the normal distribution table, The probability that the average mileage of the fleet is greater than 33.5 mpg = P(x > 33.5) = P(z > -0.66) = 1 - P(z < -0.66) = 1 - 0.2546 = 0.7454 = 74.54%