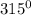Question

Musah stands at the centre of a rectangular field. He first takes 50 steps north, then 25 steps

west and finally 50 steps on a bearing of 3150

.

i. Sketch Musah’s movement

ii. How far west is Musah’s final point from the centre?
iii. How far north is Musah’s final point from the centre?

iv. Describe how you would guide a JHS student to find the bearing and distance of

Musah’s final point from the centre. ​

Answer 1

ii. 75 steps

iii. 75 steps

iv. 106 steps, and
`315^(0)`

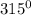
Explanation:

Let Musah's starting point be A, his waiting point after taking 50 steps northward and 25 steps westward be B, and his stopping point be C.

ii. From the second attachment, Musah's distance due west from A to C (AD) can be determined as;

bearing at B =
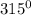`315^(0)`, therefore <BCD =
`45^(0)`

To determine distance AB,

`/AB/^(2)` =
`/50/^(2)` +
`/25/^(2)`

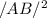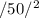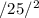
= 25000 + 625

= 3125

AB =
`√(3125)`

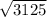
= 55.90

AB ≅ 56 steps

Thus, AC = 50 steps + 56 steps

= 106 steps

From ΔACD,

Sin
`45^(0)` =
`(x)/(106)`

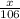
⇒ x = 106 × Sin
`45^(0)`

= 74.9533

≅ 75 steps

Musah's distance west from centre to final point is 75 steps

iii. From the secon attachment, Musah's distance north, y, can be determined by;

Cos
`45^(0)` =
`(y)/(106)`

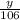
⇒ y = 106 × Cos
`45^(0)`

= 74.9533

≅ 75 steps

Musah's distance north from centre to final point is 75 steps.

iv. Musah's distance from centre to final point is AC = AB + BC

= 50 steps + 56 steps

= 106 steps

From ΔACD,

Tan θ =
`(75)/(75)`

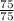
= 1.0

θ =
`Tan^(-1)` 1.0

=
`45^(0)`

Musah's bearing from centre to final point =
`45^(0)` +
`270^(0)`

=
`315^(0)`