Question

the production of a printer consists of the cost of raw material at 100 dollars the cost of overheads at 80$ and wages at 120$ if the cost of raw materials and overheads are increased by 11% and 20% respectively while wages are decreased by 15% find the percentage increase or decrease in the production cost of the printer

Answer 1

The percentage increase in the production cost of the printer is 3%.

Explanation:

We are given that the production of a printer consists of the cost of raw material at 100 dollars the cost of overheads at 80$ and wages at 120$.

Also, the cost of raw materials and overheads are increased by 11% and 20% respectively while wages are decreased by 15%.

Cost of raw material = $100

Cost of overheads = $80

Cost of wages = $120

So, the total cost of the printer = $100 + $80 + $120

= $300

Now, the increase in the cost of raw material = $100 + 11% of $100

=
`\$100 + ((11)/(100) * \$100)`

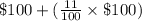
= $100 + $11 = $111

The increase in the cost of overheads = $80 + 20% of $80

=
`\$80 + ((20)/(100) * \$80)`

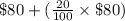
= $80 + $16 = $96

The decrease in the cost of wages = $120 - 15% of $120

=
`\$120 - ((15)/(100) * \$120)`

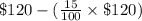
= $120 - $18 = $102

So, the new cost of a printer = $111 + $96 + $102 = $309

Now, the percentage increase in the production cost of the printer is given by;

% increase =
`\frac{\text{Net increase in the cost of printer}}{\text{Original cost of printer}} * 100`

=
`(\$309- \$300)/(\$300) * 100`

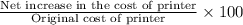
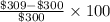
= 3%

Hence, the percentage increase in the production cost of the printer is 3%.