Question

1.Solve by factorization method: x+1/x=11 1/11 2.Comment on the nature of roots for 4x^2-5=2(〖x+1)〗^2-7 plz, help...

Answer 1

The equation

`4\,x^2-5=2\,(x+1)^2-7`

can be solved by first expanding all indicated operations, and later when the constant terms disappear, by factoring out 2x , leaving the equation as a product of two factors equal zero, from which it is easy to extract the roots. See below.

Explanation:

When solving for x in the following expression, and using factoring to apply at the end the zero product theorem:

`4\,x^2-5=2\,(x+1)^2-7\\4\,x^2-5=2\,(x^2+2x+1)-7\\4\,x^2-5=2\,x^2+4\,x+2-7\\4\,x^2-5=2\.x^2+4\,x-5\\4\,x^2=2\,x^2+4\,x\\4\,x^2-2\,x^2-4\,x=0\\2\,x^2-4\,x=0\\2\,x\,(x-2)=0`

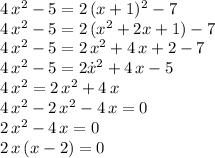
We observe that for the last product, to get a zero, x has to be zero (making the first factor zero), or x has to be "2" making the binomial factor zero.