Question

Determine the equation for the quadratic relationship graphed below.

Answer 1

`y=3x^(2) -6x-1`

Explanation:

Answer 2

`\large \boxed{\sf \bf \ \ y=3x^2-6x-1 \ \ }`

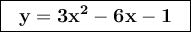
Explanation:

Hello, please consider the following.

We can read from the graph that the vertex is (1,-4) , it means that the equation is, a being a real number.

`y=a(x-1)^2-4`

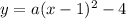
And the point (0,-1) is on the graph so we can write.

`a\cdot 1^2-4=-1 \\\\a-4+4=-1+4\\\\a = 3`

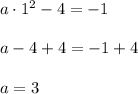
So the equation is.

`y=3(x-1)^2-4\\\\=3(x^2-2x+1)-4\\\\=3x^2-6x+3-4\\\\=3x^2-6x-1\\\\=\boxed{3}x^2\boxed{-6}x\boxed{-1}`

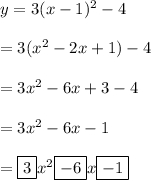
Hope this helps.

Do not hesitate if you need further explanation.

Thank you