Answer:
the probability that out of these 75 people, 14 or more drink coffee is 0.6133
Explanation:
Given that:
sample size n = 75
proportion of high school students that drink coffee p = 20% = 0.20
The proportion of the students that did not drink coffee = 1 - p
Let X be the random variable that follows a normal distribution
X
 N (n, p)
N (n, p)
X
 N (75, 0.20)
N (75, 0.20)
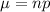 = 75 × 0.20
= 75 × 0.20
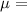 15
15
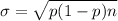
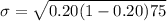
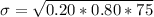

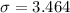
Now ; if 14 or more people drank coffee ; then
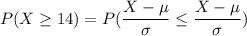
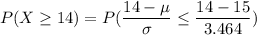

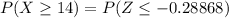
From the standard normal z tables; (-0.288)
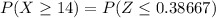
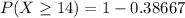
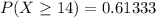
the probability that out of these 75 people, 14 or more drink coffee is 0.6133