Question

-50 points- matrix system

Answer 1

The value of X will be the following :

`\begin{bmatrix}-20\\ -5\\ -18\end{bmatrix}`

Explanation:

So as you can tell, through substitution the equation for this problem will be as follows,

`\begin{bmatrix}1&-4&-2\\ \:-2&2&5\\ \:\:\:\:\:2&-4&-2\end{bmatrix}^{^{^{^(-1)}}}\cdot \:X\:=\:\begin{bmatrix}2\\ \:\:7\\ \:-3\end{bmatrix}`

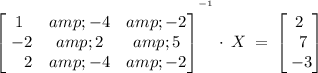
Therefore to isolate X, we have to multiply the inverse of the inverse of the co - efficient of X on either side, such that X = A
`*` B,

`X = A * B = \begin{bmatrix}1&-4&-2\\ \:\:-2&2&5\\ \:\:\:2&-4&-2\end{bmatrix}^(\:)\begin{bmatrix}2\\ 7\\ \:-3\end{bmatrix}`

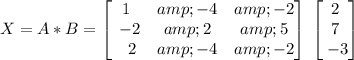
To solve for X we can multiply the rows of the first matrix by the respective columns of the second matrix,

`\begin{bmatrix}1&-4&-2\\ -2&2&5\\ 2&-4&-2\end{bmatrix}\begin{bmatrix}2\\ 7\\ -3\end{bmatrix} = \begin{bmatrix}1\cdot \:2+\left(-4\right)\cdot \:7+\left(-2\right)\left(-3\right)\\ \left(-2\right)\cdot \:2+2\cdot \:7+5\left(-3\right)\\ 2\cdot \:2+\left(-4\right)\cdot \:7+\left(-2\right)\left(-3\right)\end{bmatrix} = \begin{bmatrix}-20\\ -5\\ -18\end{bmatrix}`

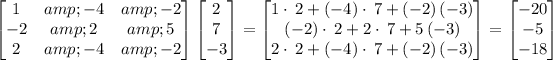
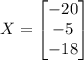`X = \begin{bmatrix}-20\\ -5\\ -18\end{bmatrix}` - if this matrix is matrix 1, matrix 1 will be our solution

Answer 2

-20

-5

-18

Explanation:

AX = B to find x

A^-1 AX = A^-1 B

X = 1 -4 -2 2

-2 2 5 * 7

2 -4 -2 -3

We multiply across and down

-1 *2 + -4 *7 -2 *-3 = -20

-2 * 2 + 2 * 7 + 5 * -3 = -5

2 * 2 -4 * 7 -2 * -3 = -18

The matrix is

-20

-5

-18