Question

Independent random samples taken on two university campuses revealed the following information concerning the average amount of money spent on textbooks during the fall semester.

University A University B
Sample Size 50 40
Average Purchase $260 $250
Standard Deviation (s) $20 $23

We want to determine if, on the average, students at University A spent more on textbooks then the students at University B.

a. Compute the test statistic.
b. Compute the p-value.
c. What is your conclusion? Let α = 0.05.

Answer 1

The calculated Z= 10/4.61 = 2.169

The P value is 0.975 .

Since the calculated value of z= 2.169 falls in the rejection region we therefore reject the null hypothesis at 5 % significance level . On the basis of this we conclude that the students at University A do not spend more on textbooks then the students at University B.

Explanation:

We set up our hypotheses as

H0 : x 1= x2 and Ha: x1 ≠ x2

We specify significance level ∝= 0.05

The test statistic if H0: x1= x2 is true is

Z =
`\frac{x_1-x_2}\sqrt(s_1^2)/(n_1)+ (s_2^2)/(n_2)`

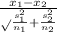
Z = 260-250/ √400/50 + 529/40

Z= 10 / √8+ 13.225

Z= 10/4.61 = 2.169

The critical value for two tailed test at alpha=0.05 is ± 1.96

The P value is 0.975 .

It is calculated by dividing alpha by 2 for a two sided test and subtracting from 1. When we subtract 0.025 ( 0.05/2)from 1 we get 0.975

Since the calculated value of z= 2.169 falls in the rejection region we therefore reject the null hypothesis at 5 % significance level . On the basis of this we conclude that the students at University A do not spend more on textbooks then the students at University B.