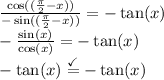Answer:
See below.
Explanation:
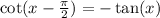
Convert the cotangent to cosine over sine:
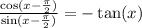
Use the cofunction identities. The cofunction identities are:
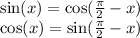
To convert this, factor out a negative one from the cosine and sine.
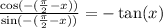
Recall that since cosine is an even function, we can remove the negative. Since sine is an odd function, we can move the negative outside: