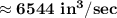Answer:
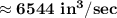
Explanation:
Given:
Rate of change of radius of cylinder:
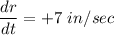
(This is increasing rate so positive)
Rate of change of height of cylinder:
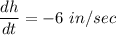
(This is decreasing rate so negative)
To find:
Rate of change of volume when r = 20 inches and h = 16 inches.
Solution:
First of all, let us have a look at the formula for Volume:

Differentiating it w.r.to 't':
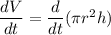
Let us have a look at the formula:
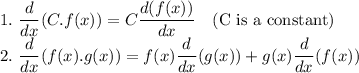
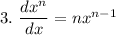
Applying the two formula for the above differentiation:

Now, putting the values:
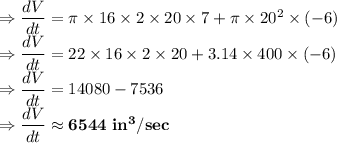
So, the answer is: