Answer:
A number line from negative 1.5 to 1.5 in increments of 0.5. A point is at 0.5 and a bold line starts at negative 0.5 and is pointing to the left.
Explanation:
Required
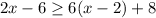
Required
Determine the number line
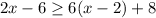
Open the bracket
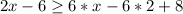
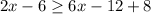
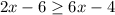
Collect Like Terms
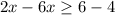
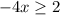
Divide both sides by -4
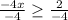
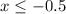
From the list of given options, the correct answer is option C