Answer:
The probability that it will take a week for it three wet weather on 3 separate days is 0.06166 and its standard deviation is 0.9447
Step-by-step explanation:
Probability of wet weather = 0.15
Probability of not being a wet weather = 1-0.15
We are supposed to find probability that it will take a week for it three wet weather on 3 separate days
Total number of days in a week = 7
We will use binomial over here
n = 7
p =probability of failure = 0.15
q = probability of success=1-0.15
r=3
Formula :
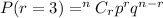
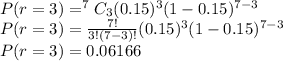
Standard deviation =
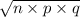
Standard deviation =

Standard deviation =0.9447
Hence The probability that it will take a week for it three wet weather on 3 separate days is 0.06166 and its standard deviation is 0.9447