Question

the rainfall R(t) (inmm) over the course of a year in bali, indonesia as a function of time t(in days) can be modeled by a sinusoidal expression of the form a*sin(b*t)+d. At t=0, in mid april, the expected daily rainfall is 2.3mm, which is the daily average value throughout the year. 1 quarter of the year leter, at t=91.25, when the rainfall is at its minimum, the expected daily value is 1.4mm. find R(t).

Answer 1

`\bold{\text{Answer:}\quad R(t)=-0.96\sin\bigg((\pi)/(182.5)t}\bigg)+2.3}`

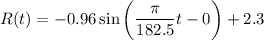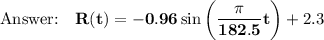
Explanation:

The equation of a sin function is: y = A sin (Bx - C) + D where

• Amplitude (A) is the distance from the midline to the max (or min)
• Period (P) = 2π/B --> B = 2π/P
• C/B is the phase shift (not used for this problem)
• D is the vertical shift (aka midline)

D = 2.3

It is given that t = 0 is located at 2.30. The sin graph usually starts at 0 so the graph has shifted up 2.3 units. --> D = 2.3

A = -0.96

The amplitude is the difference between the maximum (or minimum) and the centerline. A = 2.30 - 1.44 = 0.96

The minimum is given as the next point. Since the graph usually has the next point as its maximum, this is a reflection so the equation will start with a negative. A = -0.96

B = π/182.5

It is given that
`(1)/(4)` Period = 91.25 --> P = 365

B = 2π/P

= 2π/365

= π/182.5

C = 0

No phase shift is given so C = 0

Input A, B, C, & D into the equation of a sin function:

`R(t)=-0.96\sin\bigg((\pi)/(182.5)t-0}\bigg)+2.3`