Answer: 56.9 years to 63.1 years.
Explanation:
Confidence interval for population mean (when population standard deviation is unknown):
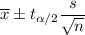
, where
 = sample mean, n= sample size, s= sample standard deviation,
= sample mean, n= sample size, s= sample standard deviation,
 = Two tailed t-value for
= Two tailed t-value for
 .
.
Given: n= 24
degree of freedom = n- 1= 23
 = 60 years
= 60 years
s= 7.4 years

Two tailed t-critical value for significance level of
 and degree of freedom 23:
and degree of freedom 23:

A 95% confidence interval on the true mean age:
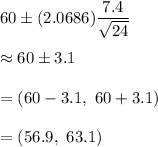
Hence, a 95% confidence interval on the true mean age. : 56.9 years to 63.1 years.