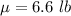Question

The mean weight of newborn infants at a community hospital is 6.6 pounds. A sample of seven infants is randomly selected and their weights at birth are recorded as 9.0, 7.3, 6.0, 8.8, 6.8, 8.4, and 6.6 pounds. Does the sample data show a significant increase in the average birthrate at a 5% level of significance?

A. Fail to reject the null hypothesis and conclude the mean is 6.6 lb.
B. Reject the null hypothesis and conclude the mean is lower than 6.6 lb.
C. Reject the null hypothesis and conclude the mean is greater than 6.6 lb.
D. Cannot calculate because the population standard deviation is unknown

Answer 1

The correct option is A

Explanation:

From the question we are told that

The population is
`\mu = 6.6`

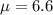
The level of significance is
`\alpha = 5\% = 0.05`

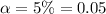
The sample data is 9.0, 7.3, 6.0, 8.8, 6.8, 8.4, and 6.6 pounds

The Null hypothesis is
`H_o : \mu = 6.6`

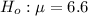
The Alternative hypothesis is
`H_a : \mu > 6.6`

The critical value of the level of significance obtained from the normal distribution table is

`Z_(\alpha ) = Z_(0.05 ) = 1.645`

Generally the sample mean is mathematically evaluated as

`\=x = (\sum x_i )/(n)`

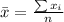
substituting values

`\=x = (9.0 + 7.3 + 6.0+ 8.8+ 6.8+ 8.4+6.6 )/(7)`

`\=x = 7.5571`

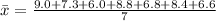
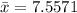
The standard deviation is mathematically evaluated as

`\sigma = \sqrt{(\sum [ x - \= x ])/(n) }`

substituting values

`\sigma = \sqrt{( [ 9.0-7.5571]^2 + [7.3 -7.5571]^2 + [6.0-7.5571]^2 + [8.8- 7.5571]^2 + [6.8- 7.5571]^2 + [8.4 - 7.5571]^2+ [6.6- 7.5571]^2 )/(7) }`
`\sigma = 1.1774`

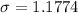
Generally the test statistic is mathematically evaluated as

`t = \frac{\= x - \mu } { (\sigma )/(√(n) ) }`

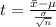
substituting values

`t = \frac{7.5571 - 6.6 } { (1.1774 )/(√(7) ) }`

`t = 1.4274`

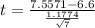
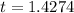
Looking at the value of t and
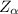`Z_(\alpha )` we see that
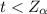`t < Z_(\alpha )` hence we fail to reject the null hypothesis

What this implies is that there is no sufficient evidence to state that the sample data show as significant increase in the average birth rate

The conclusion is that the mean is
`\mu = 6.6 \ lb`