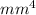Answer:
moment of inertia = 4.662 * 10^6
Step-by-step explanation:
Given data :
Mass of machine = 400 kg = 400 * 9.81 = 3924 N
length of span = 3.2 m
E = 200 * 10^9 N/m^2
frequency = 9.3 Hz
Wm ( angular frequency ) = 2
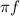 = 58.434 rad/secs
= 58.434 rad/secs
also Wm =
 ------- EQUATION 1
------- EQUATION 1
g = 9.81
deflection of simply supported beam
t =
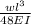
insert the value of t into equation 1
W
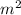 =
=
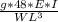 make I the subject of the equation
make I the subject of the equation
I ( Moment of inertia about the neutral axis ) =
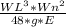
I =
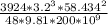 = 4.662 * 10^6
= 4.662 * 10^6