Question

PQR shown in the figure below is transformed into STU by a dilation with center (0, 0) and a scale factor of 3

Answer 1

Explanation:

Given question is incomplete; here is the complete question.

∆ PQR shown in the figure below is transformed into ∆ STU by a dilation with center (0, 0) and a scale factor of 3.

Complete the following tasks,

- Draw ΔSTU on the same set of axes.

- Fill in the coordinates of the vertices of ΔSTU.

- Complete the statement that compares the two triangles.

When ΔPQR is transformed into ΔSTU by a dilation with center (0, 0) and a scale factor of 3,

Rule to followed to get the vertices of ΔSTU,

(x, y) → (3x, 3y)

P(1, 1) → S(3, 3)

Q(3, 2) → T(9, 6)

R(3, 1) → U(9, 3)

Length of QR = 2 - 1 = 1 unit

Length of PQ =
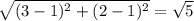`√((3-1)^2+(2-1)^2)=√(5)` units

Length of PR = 3 - 1 = 2 units

Length of ST =
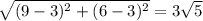`√((9-3)^2+(6-3)^2)=3√(5)` units

Length of TU = 6 - 3 = 3 units

Length of SU = 9 - 3 = 6 units

Therefore, ratio of the corresponding sides of ΔPQR and ΔSTU,

`\frac{\text{PQ}}{\text{ST}}=\frac{\text{QR}}{\text{TU}}=\frac{\text{PR}}{\text{SU}}`

`(√(5))/(3√(5))=(1)/(3)=(2)/(6)`

`(1)/(3)=(1)/(3)=(1)/(3)`

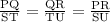
Since ratio of the corresponding sides are same,

Therefore, ΔPQR and ΔSTU are similar.