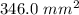Question

What the answer now now

Answer 1

The area of the triangle is
`346.0\ mm^2`

Explanation:

Given

Triangle VWU

Required

Determine the Area of the Triangle

First, we'll solve for the third angle

Angles in a triangle when added equals 180; So

`36 + 24 + <V = 180`

`60 + <V = 180`

`<V = 180 - 60`

`<V = 120`

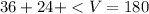
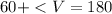
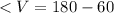
Next is to determine the length of VW using Sine Law which goes thus

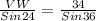`(VW)/(Sin24) = (34)/(Sin36)` (Because 24 degrees is the angle opposite side VW)

Multiply both sides by Sin24

`SIn24 * (VW)/(Sin24) = (34)/(Sin36) * Sin24`

`VW = (34)/(Sin36) * Sin24`

`VW = (34)/(0.5878) * 0.4067`

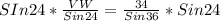
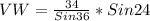
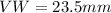`VW = 23.5 mm` (Approximated)

At this stage, we have two known sides and two known angles;

The Area can be calculated as the 1/2 * the products of two sides * Sin of the angle between the two sides

Considering VW and VU

VW = 23.5 (Calculated);

VU = 34 (Given)

The angle between these two sides is 120 (Calculated);

Hence;

`Area = (1)/(2) * 23.5 * 34 * Sin120`

`Area = (1)/(2) * 23.5 * 34 * 0.8660`

`Area = (1)/(2) * 691.934`

`Area = 346.0 mm^2`

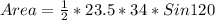
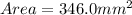
Hence, the area of the triangle is
`346.0\ mm^2`