Question

Fill in the blank with a constant, so that the resulting expression can be factored as the product of two linear expressions: 2ab-6a+5b+___ Please include an explanation too!

Answer 1

`2ab - 6a + 5b - 15`

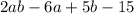
Explanation:

Given

`2ab - 6a + 5b + \_`

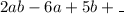
Required

Fill in the gap to produce the product of linear expressions

`2ab - 6a + 5b + \_`

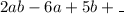
Split to 2

`(2ab - 6a) + (5b + \_)`

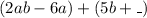
Factorize the first bracket

`2a(b - 3) + (5b + \_)`

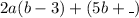
Represent the _ with X

`2a(b - 3) + (5b + X)`

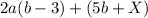
Factorize the second bracket

`2a(b - 3) + 5(b + (X)/(5))`

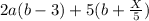
To result in a linear expression, then the following condition must be satisfied;

`b - 3 = b + (X)/(5)`

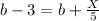
Subtract b from both sides

`b - b- 3 = b - b+ (X)/(5)`

`- 3 = (X)/(5)`

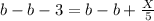
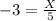
Multiply both sides by 5

`- 3 * 5 = (X)/(5) * 5`

`X = -15`

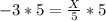
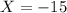
Substitute -15 for X in
`2a(b - 3) + 5(b + (X)/(5))`

`2a(b - 3) + 5(b + (-15)/(5))`

`2a(b - 3) + 5(b - (15)/(5))`

`2a(b - 3) + 5(b - 3)`

`(2a + 5)(b - 3)`

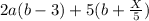
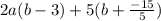
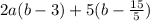
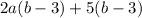
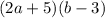
The two linear expressions are
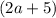`(2a+ 5)` and
`(b - 3)`

Their product will result in
`2ab - 6a + 5b - 15`

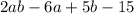
Hence, the constant is -15