Answer:
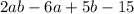
Explanation:
Given
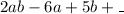
Required
Fill in the gap to produce the product of linear expressions
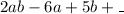
Split to 2
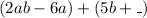
Factorize the first bracket
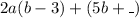
Represent the _ with X
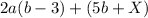
Factorize the second bracket
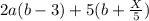
To result in a linear expression, then the following condition must be satisfied;
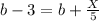
Subtract b from both sides
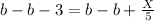

Multiply both sides by 5
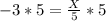

Substitute -15 for X in
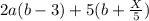
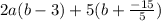

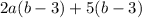
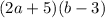
The two linear expressions are
 and
and

Their product will result in
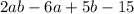
Hence, the constant is -15