Answer:
The height of the box with the smaller base is 4 times that of the box with the larger base
Explanation:
The volume of a box is the product of the base area and the height of the box, it is given as:
Volume = base area × height
For the smaller base box, it has a base of 5 cm by 5 cm, therefore the base area of the smaller base box = 5 cm × 5 cm = 25 cm². Let the height of the smaller base box be
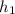 The volume of the small box =
The volume of the small box =

For the larger base box, it has a base of 10 cm by 10 cm, therefore the base area of the larger base box = 10 cm × 10 cm = 100 cm². Let the height of the large base box be
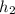 The volume of the larger base box =
The volume of the larger base box =
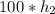
Since both boxes have the same volume, therefore:
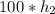 =
=

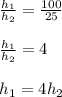
The height of the box with the smaller base is 4 times that of the box with the larger base