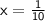4^(3/4) * 2^(x) =16^(2/5)

Question

`4^(3/4) * 2^(x) =16^(2/5)`

Answer 1

Explanation:

2^{2*3/4} × 2^{x}=2^{4×2/5}

2^{3/2} × 2^{x}= 2^{8/5}

2^{3/2+x}=2^{8/5}

equate powers

{3+2x}/2= 2^2

5{3+2x}= 2{8}

15+10x=16

collect like terms

10x=16-15

10x=1

divide both sides by 10

x=1/10

x=0.1

Answer 2

`\sf x=(1)/(10)`

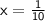
Explanation:

Rewrite expression with bases of 4.

`\sf{4^{(3)/(4) }} * \sf({4^(1)/(2) )^x =(4^2)^{(2)/(5) }`

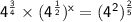
Apply law of exponents, when bases are same for exponents in multiplication, add the exponents. When a base with an exponent has a whole exponent, then multiply the two exponents.

`\sf{4^{(3)/(4) }} * \sf{4^{(1)/(2) x}=4^{(4)/(5) }`

`\sf{4^{(3)/(4) +(1)/(2) x}=4^{(4)/(5) }`

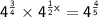
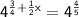
Cancel same bases.

`\sf (3)/(4) +(1)/(2) x=(4)/(5)`

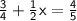
Subtract 3/4 from both sides.

`\sf (1)/(2) x=(1)/(20)`

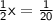
Multiply both sides by 2.

`\sf x=(1)/(10)`