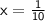Answer:
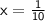
Explanation:
Rewrite expression with bases of 4.
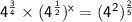
Apply law of exponents, when bases are same for exponents in multiplication, add the exponents. When a base with an exponent has a whole exponent, then multiply the two exponents.
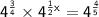
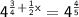
Cancel same bases.
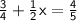
Subtract 3/4 from both sides.
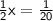
Multiply both sides by 2.