Question

Which of the following rational functions is graphed below?

Answer 1

Option (D)

Explanation:

The given graph represents a rational function having,

1). Vertical asymptote → x = 2

2). Horizontal asymptote → y = 0

Parent function representing the rational function will be in the form of,

F(x) =
`(1)/(x^(2) )`

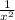
Since, vertical asymptote of the function is x = 2, denominator of the function will be in the form of (x - 2)².

Since, horizontal asymptote of the function is y = 0, highest exponent term in the numerator will be 0.

Therefore, numerator of the fraction will be x⁰.

The rational function given in the graph will be,

F(x) =
`(x^(0))/((x-2)^2)`

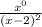
F(x) =
`(1)/((x-2)^2)`

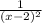
Option (D) will be the answer.